Adders and its Types

Fundamentals of Digital Arithmetic with Half Adders, Full Adders, and Their Applications

Adders are fundamental components in digital electronics and are crucial for performing arithmetic operations. In digital systems, adders are used to perform the addition of binary numbers. There are two basic types of adders: Half Adders and Full Adders.

---

Types of Adders

1. Half Adder

A Half Adder is the simplest type of adder that adds two single-bit binary numbers. It has two inputs and two outputs:

• Inputs: A and B (the bits to be added)

• Outputs: Sum and Carry

The logic equations for the Half Adder are:

• Sum (S) = A ⊕ B

• Carry (C) = A ∧ B

A Half Adder cannot add carry-in values from previous additions, making it suitable only for the least significant bit in multi-bit additions.

Here is a simple Verilog code for a half adder:

module top_module(

input a, b,

output cout, sum );

assign {cout,sum}= a+b;

endmodule

2. Full Adder

A Full Adder improves upon the Half Adder by including an additional input for the carry-in value. It can add three bits (two significant bits and one carry bit) and produce a sum and carry-out.

• Inputs: A, B, and Cin (carry-in)

• Outputs: Sum and Carry-out

The logic equations for the Full Adder are:

• Sum (S) = A ⊕ B ⊕ Cin

• Carry-out (Cout) = (A ∧ B) ∨ (Cin ∧ (A ⊕ B))

How Full Adders Work

Full adders take three inputs and produce two outputs. Here's a breakdown of how they operate:

• Sum Calculation: The sum output of a full adder is the result of the exclusive OR (XOR) operation between the three input bits. The XOR operation ensures that the sum bit is '1' when an odd number of inputs are '1'.

• Carry-Out Calculation: The carry-out output is '1' if any two or all three inputs are '1'. This is because the carry-out represents an overflow bit that is passed to the next significant bit in a multi-bit addition.

---

Types of Full Adders

Ripple Carry Adder

A Ripple Carry Adder is a simple, straightforward implementation where each full adder's carry-out is connected to the next full adder's carry-in. This means that the carry bit ripples through the adder chain, hence the name. While easy to implement, Ripple Carry Adders can be slow for large bit-widths due to the propagation delay of the carry bit through each adder.

Carry Look-Ahead Adder

A Carry Look-Ahead Adder improves the speed by reducing the carry propagation delay. It uses additional logic to calculate the carry bits in advance, based on the inputs. This allows the adder to "look ahead" and determine the carry bits much faster, significantly improving the speed of the addition operation, especially for larger bit-widths.

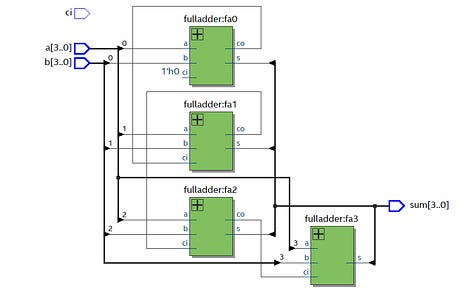
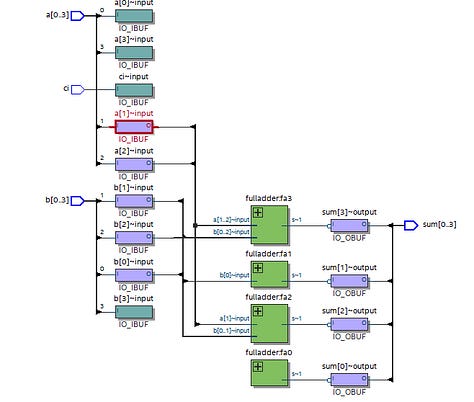
Example: The 4-Bit Full Adder

To handle larger binary numbers, multiple Full Adders can be connected in series. A 4-bit ripple carry adder is created by chaining four Full Adders together. Each Full Adder handles a single bit of the 4-bit numbers being added and passes its carry-out to the next adder in the chain.

Structure of a 4-Bit Full Adder

Inputs:

• Two 4-bit binary numbers (A and B)

• A carry-in bit (Cin)

Outputs:

• A 4-bit sum (S)

• A carry-out bit (Cout)

Each bit of the binary numbers A and B is added by a separate full adder. The carry-out from each full adder is passed to the next full adder in the sequence.

For detailed Verilog implementations, check out my GitHub repository.

The Importance of Full Adders

A full adder is crucial in digital systems because it enables the addition of larger binary numbers, which is fundamental in arithmetic operations within processors and other digital devices. By cascading full adders, more significant bits can be added, allowing for the construction of adders that handle larger data sizes.

Applications of Full Adders

• Arithmetic Logic Units (ALUs): Perform addition, subtraction, and other arithmetic operations in processors.

• Digital Systems: Essential for calculations in calculators, digital watches, and other electronic devices.

• Complex Circuits: Serve as building blocks for more complex circuits like multipliers and arithmetic circuits.

---

Interested in More Digital Design Content?

Follow me on Substack for future posts on similar topics, including detailed explanations and Verilog implementations.

Connect with Me:

• LinkedIn: Rana Umar Nadeem

• Medium: @ranaumarnadeem

• GitHub: ranaumarnadeem/HDL

• Substack: We Talk Chips

Tags: #Electrical #LogicDesign #Verilog #HDL #CombinationalLogic #FourBitAdder #DigitalDesign #FPGA #Arithmetic #ComputerEngineering#RISCV #Adder #DigitalLogic #electrical #electrical engineering